A háromszög területét kiszámolni
Innen: Hogyankell.hu
[szerkesztés] Hogyan kell a háromszög területét kiszámolni?
A háromszög területének kiszámítása az alap és a magasság ismeretében a legkönnyebb, mutatjuk, hogyan tudod egyszerűen elvégezni a számítást. A tippek között arra is hozunk megoldást, hogy ha csak a háromszög oldalainak a hossza ismert.
[szerkesztés] Lépések
- A háromszög területszámítási képlete:
- Terület = (alap * magasság) / 2
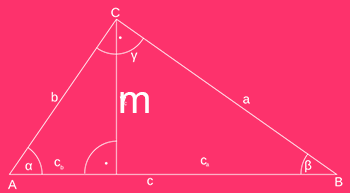
- Ez a képlet azt jelenti, hogy a háromszög alapjának hosszát szorozzuk meg a magasság hosszával, majd az eredményt osszuk el kettővel. (A fenti képen az alap a 'c' oldal, míg a magasság az 'm'-el jelölt vonal).
- Határozd meg a háromszög alapját és magasságát. A háromszög alapja az az oldal, amelyre a magasság merőleges. A magasság pedig a háromszög csúcsától indul, és merőlegesen ér a háromszög alapjára. Megjegyzendő, hogy nem minden háromszög esetében egyértelmű, melyik oldalt tekintjük alapnak, ezért előfordulhat, hogy a magasságot külön kell mérni vagy számolni.
- Szorozd össze az alap és a magasság hosszát. Ezt a szorzást gyakran írják "alap x magasság" formában.
- Oszd el a szorzatot kettővel. Ez az eljárás azt jelenti, hogy az előző lépésben kapott számot elosztjuk kettővel. Ezzel megkapod a háromszög területét.
[szerkesztés] Tippek
- Ha a háromszög oldalainak hosszát ismered, de a magasságot nem, használhatod Heron képletét is a terület kiszámítására. Ez a képlet a háromszög oldalainak hosszát használja a terület kiszámításához, és a következőképpen néz ki: Terület = √[s(s - a)(s - b)(s - c)], ahol "s" a félfogó (a + b + c) / 2, és "a", "b", és "c" a háromszög oldalainak hossza.
- Ha a háromszög derékszögű, akkor az alapot és a magasságot a derékszögű oldalak hosszaként értelmezhetjük, és használhatjuk a "terület = (alap * magasság) / 2" képletet.
[szerkesztés] Amire szükséged lehet
- A háromszög alapjának és magasságának hossza (vagy a háromszög oldalainak hossza, ha Heron képletét használod)
- Számológép (opcionális)
[szerkesztés] Figyelmeztetések
- Mindig győződj meg arról, hogy a mérések pontosak, mert a pontatlanságok hibás eredményt eredményezhetnek.
- Ha időd engedi, mindig ellenőrizd a számítást.