Deltoidot szerkeszteni
A lap korábbi változatát látod, amilyen Kiscsillag (vitalap | szerkesztései) 2012. augusztus 31., 12:48-kor történt szerkesztése után volt. (→Lépések)
Hogyan kell deltoidot szerkeszteni?
Különböző megadott paraméterek alapján bemutatjuk, hogy hogyan kell deltoidot szerkeszteni.
Lépések
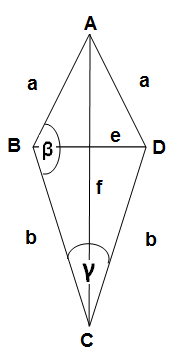
- Ha adott két oldal (a, b) és a szimmetriaátló hossza (f)
- Húzzuk meg a szimmetriaátlót, majd C pontból körzővel húzzunk egy b sugarú kört, míg A pontból egy a sugarú kört. Ahol a két kör metszi egymást, az adja meg a B és a D pontokat. Kössük össze az A és a C pontokat a B és a D pontokkal.
- Ha adott két oldal (a, b) és a közbezárt szög (β)
- Szerkesszük meg az egyik oldalt (a), majd az egyik végpontjára (B) mérjük fel β-t szögmérő segítségével. A szög másik szárán mérjük le B ponttól a b oldal hosszát, így megkapjuk a C pontot.
- Ezt követően vagy tükrözzük AC (f) egyenesre a B pontot, hogy megkapjuk a D pontot,
- Vagy A pontból körzővel AB sugarú (a) kört húzunk, míg C pontból BC sugarú (b) kört. A metszőpont megadja D-t.
- Vonalzóval a megfelelő sorrendben kössük össze a pontokat.
- Ha adott két oldala (a, b), és a hosszabb oldalak által bezárt szög (γ)
- Vegyük fel b oldalt (BC), majd a C pontnál szögmérő segítségével mérjük fel γ felét.
- B pontból körzővel húzzunk egy a sugarú kört. Ahol a kör metszi a γ szög szárát, ott kapjuk meg az A pontot.
- Ezt követően vagy tükrözzük AC (f) egyenesre a B pontot, hogy megkapjuk a D pontot,
- Vagy A pontból körzővel AB sugarú (a) kört húzunk, míg C pontból BC sugarú (b) kört. A metszőpont megadja D-t.
Tippek
- A megadott paraméterek alapján általában érdemes abból kiindulni, hogy egy háromszöget hogyan tudnál ezek alapján megszerkeszteni.
Amire szükséged lehet
- vonalzó
- körző
- szögmérő
Figyelmeztetések
- Mindig nevezd el a szögeket és az oldalakat, hogy biztosan jó legyen a szerkesztés.
Kapcsolódó források, hivatkozások
- Középiskola