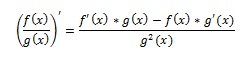„Deriválni” változatai közötti eltérés
Innen: Hogyankell.hu
(→Lépések) |
(→Amire szükséged lehet) |
||
| (12 közbenső módosítás, amit 2 másik szerkesztő végzett, nincs mutatva) | |||
| 5. sor: | 5. sor: | ||
== Lépések == | == Lépések == | ||
| − | # Legfontosabb deriválási szabályok: | + | # '''Legfontosabb deriválási szabályok:''' |
#* Konstanssal való szorzás (osztás): (c*f(x))'=c*f'(x) | #* Konstanssal való szorzás (osztás): (c*f(x))'=c*f'(x) | ||
#* Két függvény összege és különbsége: (f(x)+g(x))'=f'(x)+g'(x) és (f(x)-g(x))'=f'(x)-g'(x) | #* Két függvény összege és különbsége: (f(x)+g(x))'=f'(x)+g'(x) és (f(x)-g(x))'=f'(x)-g'(x) | ||
#* Két függvény szorzata: (f(x)*g(x))'=f'(x)*g(x)+f(x)*g'(x) | #* Két függvény szorzata: (f(x)*g(x))'=f'(x)*g(x)+f(x)*g'(x) | ||
| − | #* Két függvény hányadosa: | + | #* Két függvény hányadosa: [[Fájl:derivalas.jpg]] |
#* Összetett függvény: (f(g(x)))'=f'(g(x))*g'(x) | #* Összetett függvény: (f(g(x)))'=f'(g(x))*g'(x) | ||
| − | # Az elemi függvények deriváltjai: Az elemi függvények deriváltjai tulajdonképpen az alapfüggvények deriválási módját adják meg. Végső soron az elemi függvényekből az előző csoportban bemutatott függvényekkel végezhető műveletek segítségével áll elő az összes számunkra releváns függvény, így ezeknek a képleteknek a segítségével elvileg minden szóba jöhető függvényt tudni kell deriválni. | + | # '''Az elemi függvények deriváltjai:''' Az elemi függvények deriváltjai tulajdonképpen az alapfüggvények deriválási módját adják meg. Végső soron az elemi függvényekből az előző csoportban bemutatott függvényekkel végezhető műveletek segítségével áll elő az összes számunkra releváns függvény, így ezeknek a képleteknek a segítségével elvileg minden szóba jöhető függvényt tudni kell deriválni.[[Fájl:derivalas2.jpg]] |
== Tippek == | == Tippek == | ||
| − | + | * Ne add fel, ha elsőre nem megy! | |
| − | |||
| − | |||
| − | |||
== Amire szükséged lehet == | == Amire szükséged lehet == | ||
| − | + | * számológép | |
| − | |||
| − | |||
| − | |||
== Figyelmeztetések == | == Figyelmeztetések == | ||
| − | + | * Mindig ügyelj a műveleti sorrendek betartására! | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
== Kapcsolódó források, hivatkozások == | == Kapcsolódó források, hivatkozások == | ||
| − | + | * [http://matstat.x3.hu/pdf/oeb_anal_v02.pdf Országh Tamás: Analízis példatár] | |
| − | |||
| − | |||
| − | * [http:// | ||
[[Kategória:Oktatás]] | [[Kategória:Oktatás]] | ||
A lap jelenlegi, 2013. december 12., 09:37-kori változata
[szerkesztés] Hogyan kell deriválni?
Az alábbiakban a legfontosabb deriválási szabályokat, valamint elemi függvények deriváltjait ismerhetjük meg. A deriválási szabályok egy függvény deriválását sem teszik önmagukban lehetővé, hanem arról szólnak, hogy ha függvényekkel műveleteket végzünk, akkor hogyan kell deriválni ezekben az esetekben.
[szerkesztés] Lépések
- Legfontosabb deriválási szabályok:
- Az elemi függvények deriváltjai: Az elemi függvények deriváltjai tulajdonképpen az alapfüggvények deriválási módját adják meg. Végső soron az elemi függvényekből az előző csoportban bemutatott függvényekkel végezhető műveletek segítségével áll elő az összes számunkra releváns függvény, így ezeknek a képleteknek a segítségével elvileg minden szóba jöhető függvényt tudni kell deriválni.
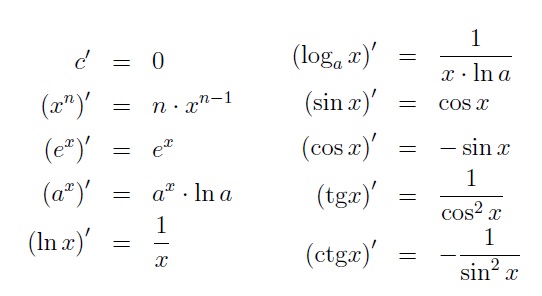
[szerkesztés] Tippek
- Ne add fel, ha elsőre nem megy!
[szerkesztés] Amire szükséged lehet
- számológép
[szerkesztés] Figyelmeztetések
- Mindig ügyelj a műveleti sorrendek betartására!